Materials+ML Workshop Day 6¶

logo

Content for today:¶

  • Types of Machine Learning
    • Supervised/Unsupervised/Reinforcement Learning
  • Supervised Learning
    • Model Validity
    • Regression, Logistic Regression, Classification
    • Train/validation/Test sets
  • Training Supervised Learning Models
    • Loss functions
    • Gradient Descent (if time)
    • Classification Problems (if time)
  • Application: Classifying Perovskites
    • Installing scikit-learn
    • scikit-learn models

The Workshop Online Book:¶

https://cburdine.github.io/materials-ml-workshop/¶

  • Recordings of Previous Workshop Sessions (and slides) now available!

Tentative Workshop Schedule:¶

Session Date Content
Day 0 06/16/2023 (2:30-3:30 PM) Introduction, Setting up your Python Notebook
Day 1 06/19/2023 (2:30-3:30 PM) Python Data Types
Day 2 06/20/2023 (2:30-3:30 PM) Python Functions and Classes
Day 3 06/21/2023 (2:30-3:30 PM) Scientific Computing with Numpy and Scipy
Day 4 06/22/2023 (2:30-3:30 PM) Data Manipulation and Visualization
Day 5 06/23/2023 (2:30-3:30 PM) Materials Science Packages
Day 6 06/26/2023 (2:30-3:30 PM) Introduction to ML, Supervised Learning
Day 7 06/27/2023 (2:30-3:30 PM) Regression Models
Day 8 06/28/2023 (2:30-3:30 PM) Unsupervised Learning
Day 9 06/29/2023 (2:30-3:30 PM) Neural Networks
Day 10 06/30/2023 (2:30-3:30 PM) Advanced Applications in Materials Science

Questions about review material:¶

  • Intro to ML Content:
    • Statistics Review
    • Linear Algebra Review

Machine Learning¶

What is Machine Learning?

Machine Learning (ML) is a subfield of AI (Artificial Intelligence), that is concerned with:

  • Developing computational models that make predictions, identify trends, etc.
  • Methods that can be applied to improve these models based on data

Google DeepMind's Alphafold (2021)¶

alphafold

OpenAI's ChatGPT and GPT-4 Models (2023):¶

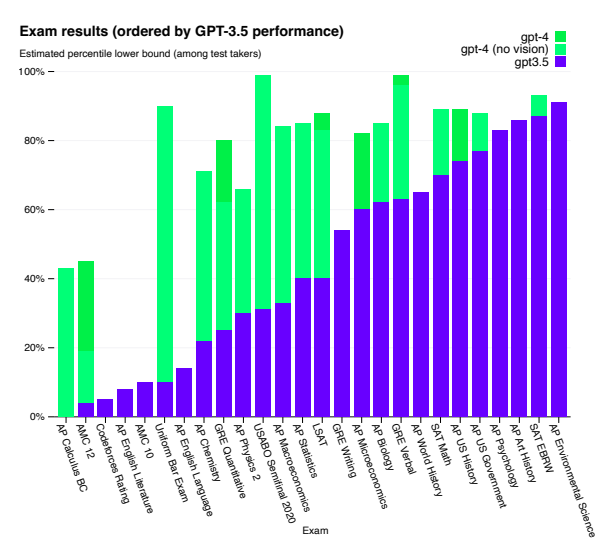
gpt4 exams

ML in Materials Science:¶

choudhary timeline

Types of Machine Learning Problems¶

Machine Learning Problems can be divided into three general categories:

  • Supervised Learning: A predictive model is provided with a labeled dataset with the goal of making predictions based on these labeled examples
    • Examples: regression, classification
  • Unsupervised Learning: A model is applied to unlabeled data with the goal of discovering trends, patterns, extracting features, or finding relationships between data.
    • Examples: clustering, dimensionality reduction, anomaly detection
  • Reinforcement Learning: An agent learns to interact with an environment in order to maximize its cumulative rewards.
    • Examples: intelligent control, game-playing, sequential design

Supervised Learning¶

When can supervised learning be applied?

  • Problems where the available data contains many different labeled examples

  • Problems that involve finding a model that maps a set of features (inputs) to labels (outputs).

  • A supervised learning dataset consists of $(\mathbf{x}, y)$ pairs:

    • $\mathbf{x}$ is a vector of features (model inputs)
    • $y$ is a label to be predicted (the model output)

  • $y$ values can be continuous scalars, vectors, or discrete classes.

  • Here, we will assume $\mathbf{x}$ is a real vector and $y$ is a continuous real scalar (unless otherwise specficied).

What is the goal of supervised Learning?

  • The goal is to learn a model that makes accurate predictions (denoted $\hat{y}$) of $y$ based on a vector of features $\mathbf{x}$.

  • We can think of a model as a function $f : \mathcal{X} \rightarrow \mathcal{Y}$

    • $\mathcal{X}$ is the space of all possible feature vectors $\mathbf{x}$
    • $\mathcal{Y}$ is the space of all labels $y$.

function

Types of Supervised Learning Problems:¶

The type of a supervised learning problem depends on the type of value $y$ we are attempting to predict:

  • If $y$ is a continuous value, it is a regression problem

  • If $y$ can be a finite number of values, it is a classification problem

  • If $y$ is a continuous probability (between $0$ and $1$), it is a logistic regression problem*

*In some textbooks, logistic regression also refers to a specific kind of model that is used for predicting probabilities.

Model Validity¶

  • A model $f: \mathcal{X} \rightarrow \mathcal{Y}$ is valid if it approximately maps every set of features in $\mathcal{X}$ to the correct label $\mathcal{Y}$:
$$ \hat{y} = f(\mathbf{x}) \approx y$$
  • This must hold for every label $y$ associated with every possible feature vector $\mathbf{x}$ in $\mathcal{X}$.

Model validity is a subjective property, because we may not know what the correct label $y$ is for every single value $\mathbf{x}$ in $\mathcal{X}$.

  • Example: classifying images of cats vs. dogs

catdog

  • Often, we only know the $(\mathbf{x},y)$ pairs in our dataset.

  • If there is noise or bias in our data, even those $(\mathbf{x},y)$ pairs may be unreliable.

  • Even if a model fits the dataset perfectly, we may not know if the fit is valid, because we don't know the $(\mathbf{x},y)$ pairs that lie outside the training dataset:

supervised model ood

Choosing between two models:¶

  • Consider the following two models fit to the same dataset:

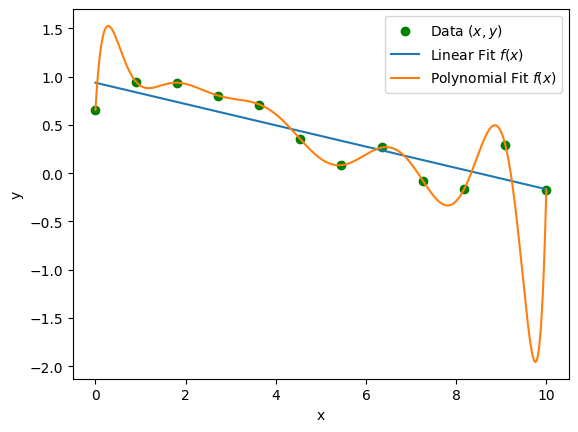
supervised model example

Which model is the more valid model?

  • Even though the polynomial perfectly fits the data, it is not valid because it extrapolates poorly:

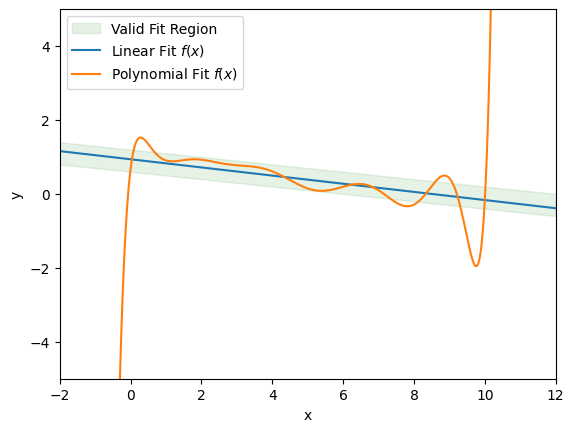
fit extrapolations

Estimating Validity:¶

Here's how we can solve the problem of estimating model validity:

  • Purposely leave out a random subset of the data that the model is fit to.

    • Use that subset to evaluate the accuracy of the fitted model.

  • This subset that we leave out is called the validation set.

  • The subset we fit the model to is called the training set.

Traning Validation, and Test Sets:¶

  • Common practice is to set aside 10% of the data as the validation set.
  • In some problems another 10% of the data is set aside as the test set.

supervised split

Validation vs. Test Sets:¶

  • The validation set is used for comparing the accuracy of different models or instances of the same model with different parameters.

  • The test set is used to provide a final, unbiased estimate of the best model selected using the validation set.

  • Evaluating the final model accuracy on the test set eliminates selection bias associated with the accuracies on the validation set.

    • The more models that are compared using the validation set, the greater the need for the test set.

    • This is especially true if you are reporting the statistical significance of your model's accuracy being better than another model.

Preparing Data:¶

  • For each feature vector $\mathbf{x}$, some features vary much more than other features.

  • To avoid making our model more sensitive to features with high variance, we normalize each feature, so that it lies roughly on the interval $[-2,2]$.

  • Normalization is a transformation $\mathbf{x} \mapsto \mathbf{z}$:
$$z_i = \frac{x_i - \mu_i}{\sigma_i}$$
  • $\mu_i$ and $\sigma_i$ are the mean and standard deviation of the $i$th feature in the training dataset.

Loss functions:¶

  • To evaluate the accuracy of a model on a dataset, we use a loss function.

  • A loss function is function of a prediction $\hat{y}$ and a true label $y$ that increases as the prediction deviates from the true label.

  • Example (square error loss):
$$E(\hat{y}, y) = (\hat{y} - y)^2$$
  • A good loss function should attain its minimum when $\hat{y} = y$.

Model Loss Functions:¶

  • We can evaluate how well a model $f$ fits a dataset $\{(\mathbf{x}_i, y_i)\}_{i=1}^N$ by taking the average of a loss function evaluated on all $(\mathbf{x}_i, y_i)$ pairs.

Examples:

  • Mean Square Error (MSE):

    $$\mathcal{E}(f) = \frac{1}{N} \sum_{n=1}^N (f(\mathbf{x}_n) - y_n)^2$$

  • Mean Absolute Error (MAE):

    $$\mathcal{E}(f) = \frac{1}{N} \sum_{n=1}^N |f(\mathbf{x}_n) - y_n|$$

  • Classification Accuracy:

    $$\mathcal{E}(f) = \frac{1}{N} \sum_{n=1}^N \delta(\hat{y} - y) = \left[ \frac{\text{# Correct}}{\text{Total}} \right]$$

Fitting Models to Data:¶

  • Most models have weights that must be adjusted to fit the training dataset:

  • Example (1D polynomial regression):

    $$f(x) = \sum_{d=0}^{D} w_dx^d$$

  • There are many different methods that can be used to find the optimial weights $w_i$.

  • The most common method for fitting the data is through gradient descent.

    • Gradient descent makes iterative adjustments to weight values such that each adjustment decreases the model loss $\mathcal{E}(f)$.

  • Some models (such as linear regression) have optimal weights that can be solved for in closed form.

Gradient Descent¶

  • Gradient descent makes iterative adjustments to the model weights $\mathbf{w}$:
$$\mathbf{w}^{(t+1)} = \mathbf{w}^{(t)} - \nabla_w \mathcal{E}(f)$$

gradient descent

Review: The Gradient¶

The gradient of a function $g: \mathbb{R}^n \rightarrow \mathbb{R}$ is the vector-valued function:

$$\nabla g(\mathbf{w}) = \begin{bmatrix} \frac{\partial g}{\partial w_0}(\mathbf{w}) & \frac{\partial g}{\partial w_1}(\mathbf{w}) & \dots & \frac{\partial g}{\partial w_n}(\mathbf{w}) \end{bmatrix}^T$$
  • ($\nabla g(\mathbf{w})$ is a function $\mathbb{R}^n \rightarrow \mathbb{R}^n$)
  • The gradient at a point $\mathbf{w}$ "points" in the direction in which $g$ increases the most.

Tutorial: Classifying Perovskites¶

  • We will work with some basic classification models that classify perovskite materials as "cubic" or "non-cubic".

Recommended Reading:¶

  • Advanced Regression Models

If possible, try to do the exercises. Bring your questions to our next meeting (next Monday).