Materials+ML Workshop Day 8¶

logo

Content for today:¶

  • Regression Models Review

    • Linear Regression
    • High-dimensional Embeddings
    • Kernel Machines

  • Unsupervised Learning

    • Feature Selection
    • Dimensionality reduction
    • Clustering
    • Distribution Estimation
    • Anomaly Detection

  • Application: Classifying Superconductors

    • Application of unsupervised methods

Tentative Workshop Schedule:¶

Session Date Content
Day 0 06/16/2023 (2:30-3:30 PM) Introduction, Setting up your Python Notebook
Day 1 06/19/2023 (2:30-3:30 PM) Python Data Types
Day 2 06/20/2023 (2:30-3:30 PM) Python Functions and Classes
Day 3 06/21/2023 (2:30-3:30 PM) Scientific Computing with Numpy and Scipy
Day 4 06/22/2023 (2:30-3:30 PM) Data Manipulation and Visualization
Day 5 06/23/2023 (2:30-3:30 PM) Materials Science Packages
Day 6 06/26/2023 (2:30-3:30 PM) Introduction to ML, Supervised Learning
Day 7 06/27/2023 (2:30-3:30 PM) Regression Models
Day 8 06/28/2023 (2:30-3:30 PM) Unsupervised Learning
Day 9 06/29/2023 (2:30-3:30 PM) Neural Networks
Day 10 06/30/2023 (2:30-3:30 PM) Advanced Applications in Materials Science

Questions¶

  • Regression Models
    • Linear Regression
    • High-dimensional Embeddings
    • Kernel Machines
    • Supervised Learning (in general)

Multivariate Linear Regression¶

  • Multivariate Linear regression is a type of regression model that estimates a label as a linear combination of features:
$$\hat{y} = f(\mathbf{x}) = w_0 + \sum_{i=1}^D w_i x_i$$

  • We can re-write the linear regression model in vector form:

    • Let $\underline{\mathbf{x}} = \begin{bmatrix} 1 & x_1 & x_2 & \dots & x_D \end{bmatrix}^T$ ($\mathbf{x}$ padded with a 1)
    • Let $\mathbf{w} = \begin{bmatrix} w_0 & w_1 & w_2 & \dots & w_D \end{bmatrix}^T$ (the weight vector)
  • $f(\mathbf{x})$ is just the inner product (i.e. dot product) of these two vectors:
$$\hat{y} = f(\mathbf{x}) = \underline{\mathbf{x}}^T\mathbf{w}$$

Closed Form Solution:¶

  • Multivariate Linear Regression:
$$\mathbf{w} = \mathbf{X}^+\mathbf{y}$$
  • Above, $\mathbf{X}^+$ denotes the Moore-Penrose inverse (sometimes called the pseudo-inverse) of $\mathbf{X}$.
  • If the dataset size $N$ is sufficiently large such that $\mathbf{X}$ has linearly independent columns, the optimal weights can be computed as:
$$\mathbf{w} = \mathbf{X}^{+}\mathbf{y} = \left( (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\right)\mathbf{y}$$

High-Dimensional Embeddings¶

  • Often, the trends of $y$ with respect to $\mathbf{x}$ are non-linear, so multivariate linear regression may fail to give good results.

  • One way of handling this is by embedding the data in a higher-dimensional space using many different non-linear functions:

$$\phi_j(\mathbf{x}) : \mathbb{R}^{D} \rightarrow \mathbb{R}\qquad (j = 1, 2, ..., D_{emb})$$

(The $\phi_j$ are nonlinear functions, and $D_{emb}$ is the embedding dimension)

$$\hat{y} = f(\mathbf{x}) = w_0 + \sum_{j=1}^{D_{emb}} w_j \phi_j(\mathbf{x})$$

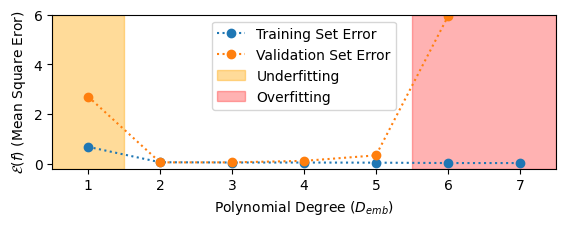
Underfitting and Overfitting¶

  • Finding the best fit of a model requires striking a balance between underfitting and overfitting the data.
  • A model underfits the data if it has insufficient degrees of freedom to model the data.
  • A model overfits the data if it has too many degrees of freedom such that it fails to generalize well outside of the training data.

Polynomial Regression Example:

poly fits

Regularization:¶

  • To reduce overfitting, we apply regularization:

  • Usually, a penalty term is added to the overall model loss function:

    $$\text{ Penalty Term } = \lambda \sum_{j} w_j^2 = \lambda(\mathbf{w}^T\mathbf{w})$$

  • The parameter $\lambda$ is called the regularization parameter

    • as $\lambda$ increases, more regularization is applied.

Today's Content:¶

Unsupervised Learning

  • Feature Selection
  • Dimensionality reduction
  • Clustering
  • Distribution Estimation
  • Anomaly Detection

Unsupervised Learning Models:¶

  • Models applied to unlabeled data with the goal of discovering trends, patterns, extracting features, or finding relationships between data.
    • Deals with datasets of features only
    • (just $\mathbf{x}$, not $(\mathbf{x},y)$ pairs)

unsupervised learning

Feature Selection and Dimensionality Reduction¶

  • Determines which features are the most "meaningful" in explaining how the data is distributed

  • Sometimes we work with high-dimensional data that is very sparse

  • Reducing the dimensionality of the data might be necessary

    • Reduces computational complexity
    • Eliminates unnecessary (or redundant) features
    • Can even improve model accuracy

The Importance of Dimensionality¶

  • Dimensionality is an important concept in materials science.
    • The dimensionality of a material affects its properties
  • Much like materials, the dimensionality of a dataset can say a lot about the properties of a dataset:
    • How complex is the data?
    • Does the data have fewer degrees of freedom than features?
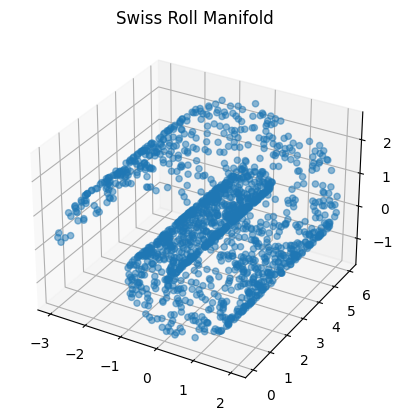
  • Sometimes, data can be confined to some low-dimensional manifold embedded in a higher-dimensional space.

Example: The "Swiss Roll" manifold

Swiss roll

Review: The Covariance Matrix¶

  • The Covariance Matrix describes the variance of data in more than one dimension:
$$\mathbf{\Sigma} = \begin{bmatrix} \sigma_{1}^2 & \sigma_{12} & \dots & \sigma_{1d} \\ \sigma_{21} & \sigma_{2}^2 & \dots & \sigma_{2d} \\ \vdots & \vdots & \ddots & \vdots \\ \sigma_{d1} & \sigma_{d2} & \dots & \sigma_{d}^2 \end{bmatrix}$$
  • $\Sigma_{ii} = \sigma_i^2$: variance in dimension $i$
  • $\Sigma_{ij} = \sigma_{ij}$: covariance between dimensions $i$ and $j$
$$\Sigma_{ij} = \frac{1}{N} \sum_{n=1}^N ((\mathbf{x}_n)_i - \mu_i)((\mathbf{x}_n)_j - \mu_j)$$

The Correlation Matrix:¶

  • Recall that it is generally a good idea to normalize our data:
$$\mathbf{x} \mapsto \mathbf{z}:\quad z_i = \frac{x_i - \mu_i}{\sigma_i}$$
  • The correlation matrix (denoted $\bar{\Sigma}$) is the covariance matrix of the normalized data:
$$ \bar{\Sigma} = \frac{1}{N} \sum_{n=1}^N \mathbf{z}_n\mathbf{z}_n^T $$
  • The entries of the correlation matrix (in terms of the original data) are:
$$\bar{\Sigma}_{ij} = \frac{1}{N} \sum_{n=1}^N \frac{((\mathbf{x}_n)_i - \mu_i)((\mathbf{x}_n)_j - \mu_j)}{\sigma_i\sigma_j}$$

Interpreting the Correlation Matrix¶

$$\bar{\Sigma}_{ij} = \frac{1}{N} \sum_{n=1}^N \frac{((\mathbf{x}_n)_i - \mu_i)((\mathbf{x}_n)_j - \mu_j)}{\sigma_i\sigma_j}$$
  • The diagonal of the correlation matrix consists of $1$s. (Why?)
  • The off-diagonal components describe the strength of correlation between feature dimensions $i$ and $j$
    • Positive values: positive correlation
    • Negative values: negative correlation
    • Zero values: no correlation

Principal Components Analysis (PCA)¶

  • The eigenvectors of the correlation matrix are called principal components.

  • The associated eigenvalues describe the proportion of the data variance in the direction of each principal component.

$$\bar{\Sigma} = P D P^{T}$$
  • $D$: Diagonal matrix (eigenvalues along diagonal)
  • $P$: Principal component matrix (columns are principal components)
  • Since $\bar{\Sigma}$ is symmetric, the principal components are all orthogonal.

Dimension reduction with PCA¶

We can project our (normalized) data onto the first $n$ principal components to reduce the dimensionality of the data, while still keeping most of the variance:

$$\mathbf{z} \mapsto \mathbf{u} = \begin{bmatrix} \mathbf{z}^T\mathbf{p}^{(1)} \\ \mathbf{z}^T\mathbf{p}^{(2)} \\ \vdots \\ \mathbf{z}^T\mathbf{p}^{(n)} \\ \end{bmatrix}$$

Clustering and Distribution Estimation¶

  • Clustering methods allow us to identify dense groupings of data.

  • Distribution Estimation allows us to estimate the probability distribution of the data.

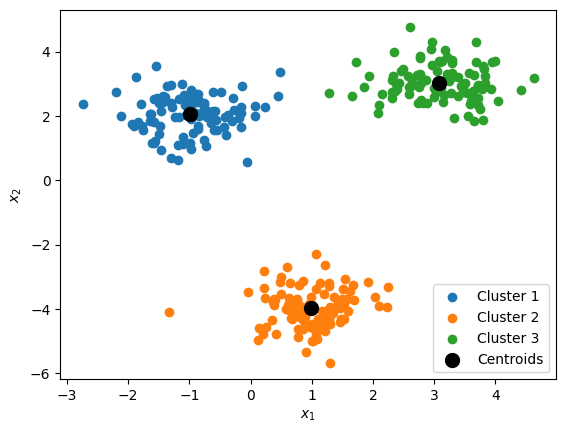
K-Means Clustering:¶

  • $k$-means is a popular clustering algorithm that identifies the centerpoints a specified number of clusters $k$

  • These center points are called centroids

kmeans

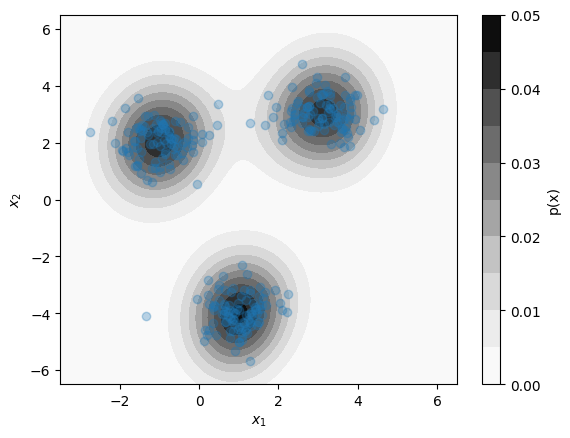
Kernel Density Estimation:¶

  • Kernel Density Estimation (KDE) estimates the probability distribution of an entire dataset

  • Estimates the distribution as a sum of multivariate normal "bumps" at the position of each datapoint

kde

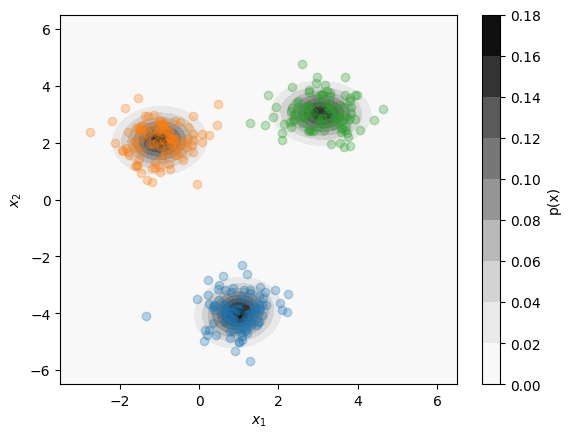
Gaussian Mixture Model¶

  • A Gaussian Mixture Model (GMM) performs both clustering and distribution estimation simultaneously.

  • Works by fitting a mixture of multivariate normal distributions to the data

gmm

Application: Classifying Superconductors¶

  • Exploring the distribution of superconducting materials

Recommended Reading:¶

  • Neural Networks

(Note: some sections are still in progress ☹️)

If possible, try to do the exercises. Bring your questions to our next meeting tomorrow.