Materials+ML Workshop Day 9

Content for today:

• Unsupervised Learning review:

  • Correlation Matrices
  • Dimensionality reduction
  • Principal Components Analysis (PCA)
  • Clustering
  • Distribution Estimation

• Neural networks:

  • Introduction to Neural Networks
  • Neuron Models
  • Activation Functions
  • Training Neural Networks

• Application:

  • Training a basic neural network with Pytorch

Tentative Workshop Schedule:

Session	Date	Content
Day 0	06/16/2023 (2:30-3:30 PM)	Introduction, Setting up your Python Notebook
Day 1	06/19/2023 (2:30-3:30 PM)	Python Data Types
Day 2	06/20/2023 (2:30-3:30 PM)	Python Functions and Classes
Day 3	06/21/2023 (2:30-3:30 PM)	Scientific Computing with Numpy and Scipy
Day 4	06/22/2023 (2:30-3:30 PM)	Data Manipulation and Visualization
Day 5	06/23/2023 (2:30-3:30 PM)	Materials Science Packages
Day 6	06/26/2023 (2:30-3:30 PM)	Introduction to ML, Supervised Learning
Day 7	06/27/2023 (2:30-3:30 PM)	Regression Models
Day 8	06/28/2023 (2:30-3:30 PM)	Unsupervised Learning
Day 9	06/29/2023 (2:30-3:30 PM)	Neural Networks
Day 10	06/30/2023 (2:30-3:30 PM)	Advanced Applications in Materials Science

Questions

• Unsupervised Learning review:
  • Feature selection
  • Correlation Matrices
  • Dimensionality reduction
  • Principal Components Analysis (PCA)
  • Clustering
  • Distribution Estimation

Unsupervised Learning Models:

• Models applied to unlabeled data with the goal of discovering trends, patterns, extracting features, or finding relationships between data.

The Importance of Dimensionality

• Dimensionality is an important concept in materials science.
  • The dimensionality of a material affects its properties

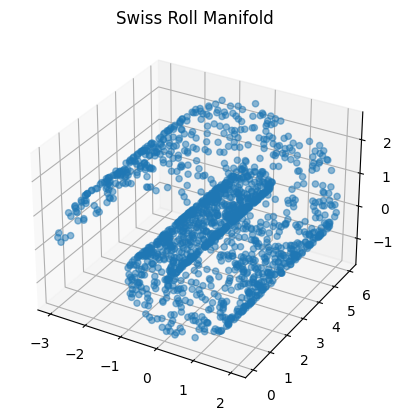
• Sometimes, data can be confined to some low-dimensional manifold embedded in a higher-dimensional space.

Example: The "Swiss Roll" manifold

The Correlation Matrix:

• Recall that it is generally a good idea to normalize our data:

$$\mathbf{x} \mapsto \mathbf{z}:\quad z_i = \frac{x_i - \mu_i}{\sigma_i}$$

• The correlation matrix (denoted $\bar{\Sigma}$) is the covariance matrix of the normalized data:

$$ \bar{\Sigma} = \frac{1}{N} \sum_{n=1}^N \mathbf{z}_n\mathbf{z}_n^T $$

Principal Components Analysis (PCA)

• The eigenvectors of the correlation matrix are called principal components.

• The associated eigenvalues describe the proportion of the data variance in the direction of each principal component.

$$\bar{\Sigma} = P D P^{T}$$

• $D$: Diagonal matrix (eigenvalues along diagonal)
• $P$: Principal component matrix (columns are principal components)

Dimension reduction with PCA

We can project our (normalized) data onto the first $n$ principal components to reduce the dimensionality of the data, while still keeping most of the variance:

$$\mathbf{z} \mapsto \mathbf{u} = \begin{bmatrix} \mathbf{z}^T\mathbf{p}^{(1)} \\ \mathbf{z}^T\mathbf{p}^{(2)} \\ \vdots \\ \mathbf{z}^T\mathbf{p}^{(n)} \\ \end{bmatrix}$$

K-Means Clustering:

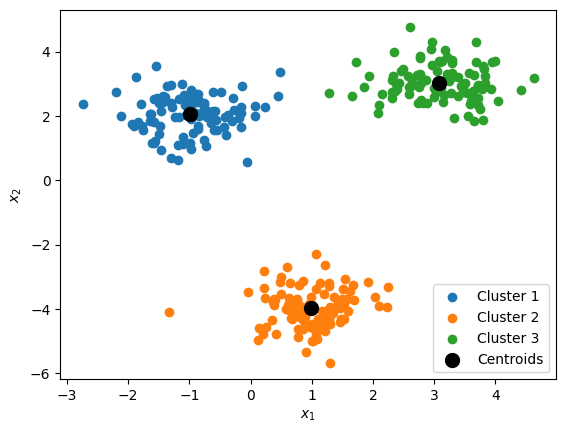
• Identifies the centerpoints for a specified number of clusters $k$

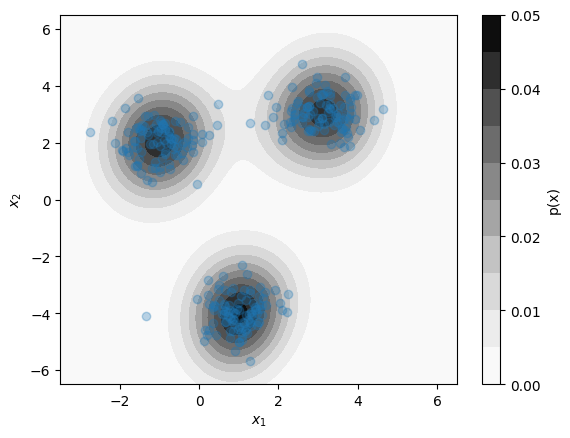
Kernel Density Estimation:

• Estimates the distribution of data as a sum of multivariate normal "bumps" at the position of each datapoint

Today's Content:

Neural Networks

• Introduction to Neural Networks

  • Neuron Models
  • Activation Functions
  • Training Neural Networks

• Application:

  • Training a basic neural network with Pytorch

Neural Networks

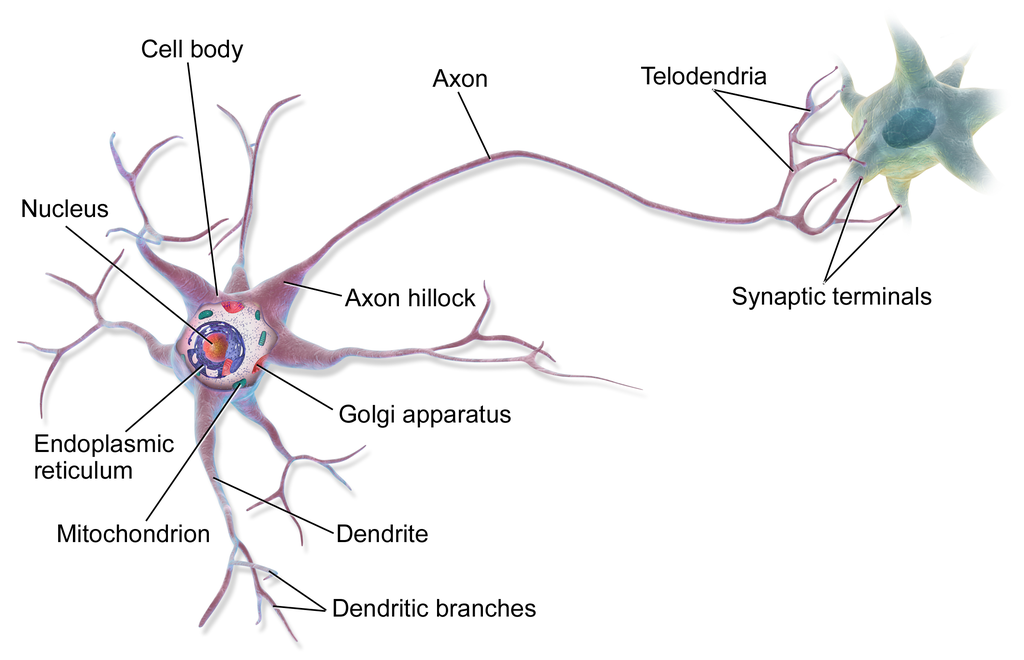
• Neural networks are supervised machine learning models inspired by the functionality of networks of multipolar neurons in the brain:

What can neural networks do?

• They are flexible non-linear models capable of solving many difficult supervised learning problems

• They often work best on large, complex datasets

• This predictive power comes at the cost of model interpretability.

• We know how the model computes predictions, but coming up with a general answer as to why a neural network makes a particular prediction is very hard.

Example: The AlphaGo Model

Standard Feed-Forward Neural Network

• Neural Networks typically consist of individual collections of "neurons" that are stacked into sequential layers:

• Example: Standard "feed-forward" neural network"

A Single Neuron:

• We have alreacy encountered a simple model of a neuron in the form of the Perceptron classifier model:

$$f(\mathbf{x}) = \text{sign}\left( w_0 + \sum_{i=1}^D w_ix_i \right)$$

($\text{sign}(x) = \pm 1$, depending on the sign of $x$)

• $f(x) = +1$ only if a weighted sum of the inputs $x_i$ exceed a given threshold (i.e. $-w_0$)

• This is similar to the electrical response of a neuron to external stimuli

• The Perceptron neuron model has some disadvantages:

  • the function $\text{sign}(x)$ is not continuous and has a derivative of 0 everywhere.

  • It can be difficult to fit this function to data if it is not continuous and differentiable.

The Neuron Activation Function

Instead of the $\text{sign}(x)$ function, we apply a continuous, non-linear function $\sigma(x)$ to the output:

• The function $\sigma(x)$ is called the neuron's activation function.

• The general form of a single neuron can be written as follows:

$$f(\mathbf{x}) = \sigma(\mathbf{w}^T\underline{\mathbf{x}}) = \sigma\left( w_0 + \sum_{i=1}^D w_ix_i \right)$$

• Recall: $\underline{\mathbf{x}} = \begin{bmatrix} 1 & x_1 & x_2 & \dots & x_D \end{bmatrix}^T$
• Also: $\mathbf{w} = \begin{bmatrix} w_0 & w_1 & w_2 & \dots & x_D \end{bmatrix}^T$

• We can choose different activations $\sigma(x)$, depending on the desired output range of the neuron.

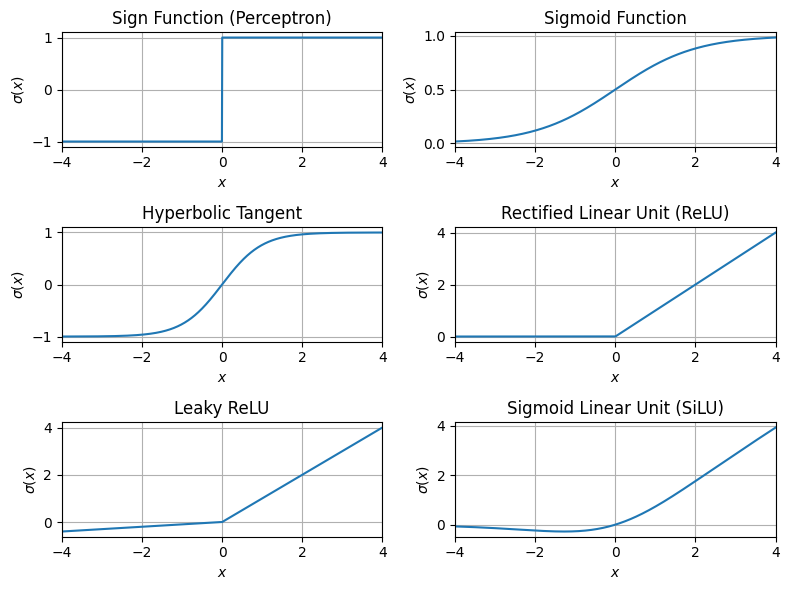
Common Activation Functions:

• Sigmoid function:

$$\sigma(x) = \frac{1}{1 + e^{-x}}$$

• Hyperbolic Tangent:

$$\sigma(x) = \tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$$

• Rectified Linear Unit (ReLU):

$$\sigma(x) = \begin{cases} x & x > 0 \\ 0 & x \le 0 \end{cases}$$

• Leaky ReLU:

$$\sigma(x) = \begin{cases} x & x > 0 \\ \alpha x & x \le 0\end{cases}\qquad (0 < \alpha \ll 1)$$

Visualizing Activation Functions

A Layer of Neurons:

• We can combine multiple independent neurons into a layer of neurons.

• The layer computes a vector $\mathbf{a} = f(\mathbf{x})$ of outputs from the neurons:

$$\mathbf{a} = \begin{bmatrix} a_1 \\ a_2 \\ \vdots \\ a_m \end{bmatrix} = f(\mathbf{x}) = \begin{bmatrix} \sigma\left(w_{1,0} + \sum_{i=1}^D w_{1,i}x_i\right) \\ \sigma\left(w_{2,0} + \sum_{i=1}^D w_{2,i}x_i\right) \\ \vdots \\ \sigma\left(w_{m,0} + \sum_{i=1}^D w_{m,i}x_i\right) \end{bmatrix}$$

• Consider a layer of $m$ neurons each with $D+1$ weights.

• We can organize the layer's weights into a matrix $\mathbf{W}$:

$$\mathbf{W} = \begin{bmatrix} w_{10} & w_{11} & \dots & w_{1D} \\ w_{20} & w_{12} & \dots & w_{2D} \\ \vdots & \vdots & \ddots & \vdots \\ w_{m0} & w_{m1} & \dots & w_{mD} \end{bmatrix}$$

• In terms of the weight matrix, we can write the neuron layer function as:

$$\mathbf{a} = f(\mathbf{x}) = \sigma(\mathbf{W}\mathbf{x})$$

The Standard Feed-Forward Neural Network

Training Neural Networks

• We train neural networks through gradient descent

$$\mathbf{w}^{(t+1)} = \mathbf{w}^{(t)} + \eta \frac{-\nabla_w \mathcal{E}(f)}{\lVert{-\nabla_w \mathcal{E}(f)}\rVert}$$

• $\eta$ is a constant called the learning rate.

• The numerical process by which $\nabla_w \mathcal{E}(f)$ for layered neural networks is computed is called backpropagation

Tutorial: Basic Neural Network in Pytorch

Goal: Train a neural network to learn the function:

$$f(x_1, x_2) = \frac{\sin(\sqrt{x_1^2 + x_2^2})}{\sqrt{x_1^2 + x_2^2}}$$

Recommended Reading:

(None)

Note: some sections of the online book are still in progress ☹️