Intro to Quantum Mechanics (Part I)
Published:
Depending on the degree of experience you have with physics, you may or may not have encountered a few concepts from quantum mechanics in your college physics or chemistry class. Often, the way that quantum mechanics is first introduced to students is through some of the key experiments in which we observe some aspect of so-called “quantum weirdness”. Somehow, when we take a peek at the world of very tiny things, we tend to observe phenomena that we would never expect to see on the scale at which we experience the everyday world. In this multiple-part blog post, I will give a survey of the basic principles of quantum mechanics and show how it has changed our perspective on the macroscopic world.
What is Quantum Mechanics?
So, what exactly is Quantum Mechanics? Physicists tend to think of Quantum Mechanics as a framework for for describing the physics of very small objects (such as protons, electrons, etc. ) and how these objects interact. Mathematicians say that Quantum Mechanics arises as the study of wave-like systems and how they can be described simply through abstract mathematical tools, such as complex numbers, algebraic fields, and Hilbert Spaces. Statisticians may offer up yet another interpretation, stating that Quantum Mechanics is simply a generalization of classical statistics (which deals with real-valued probability distributions) to wave-like systems (which deal with complex-valued probability distributions). A common theme that unites these three perspectives is that Quantum Mechanics is characterized by a shift away from the idea that everything about a system can be known and toward the idea there are certain trade-offs concerning what can and cannot be learned about a system through observation.
Before the advent of quantum mechanics in modern physics, it was widely believed that the physical world could be modeled by a combination of discrete particles (such as protons, electrons, and neutrons) interacting at a distance through invisible fields with wave-like behavior. These fields were responsible for forces between particles, such as the attraction between opposite poles of a magnet and the propagation of light. At the time, it was understood that there was no gray area between wave-like fields and particles. All observable physical objects were either one or the other.
It wasn’t until the early 20th century that this understanding of a strict particle-wave dichotomy was brought into question. In 1900, the physicist Max Planck discovered that the measured energies for the frequencies of light radiated by objects were not continuous in nature; rather, they were discrete. Planck went on to postulate that light itself was emitted in discrete packets, which Planck called quanta. For light emitted at a frequency $\nu$, Planck showed experimentally that the energy emitted was in multiples of $h\nu$ where $h = 6.626 \cdot 10^{-34}$ J/Hz. The energy $E$ of a single quantum of light is then given by Planck’s equation: \(E = h\nu\) The quantity $h$ is known today as Planck’s constant, and is one of the fundamental constants of nature.
Planck’s discovery showed that fields of electromagnetic radiation that were once believed to be continuous come in discrete units of energy. This discretization suggested that light had properties like that of particles because its quanta could be counted. Today, physicists refer to these packets of light energy as photons. In 1924, another physicist, Louis de Broglie, postulated that particles with mass, such as electrons, could exhibit wavelike behavior. Specifically, his postulate suggested that if light quanta have momentum $p = E/c$ (where $c$ is the speed of light), then one could apply this same relationship to particles with mass, thereby obtaining the “wavelength” $\lambda$ of a particle:
\[p = \frac{E}{c} = \frac{h\nu}{c} = \frac{h\nu}{(\nu \lambda)} = \frac{h}{\lambda}\quad \Rightarrow\quad \lambda = h/p\]Remarkably, de Broglie’s prediction of the existence of a “matter wave” turned out to be correct, and has since been verified through many experiments, such as the famous electron double-slit experiment. These experiments showed that particles with mass can also have wave-like properties, exhibiting interference patterns that are not seen in classical particles.
As experimental evidence continued to blur the lines between what were once considered to be particles and waves, the field of Quantum Mechanics was born. This new field of physics sought to unite the particle and wave-like nature of objects with “quantized” energy into a single mathematical framework. In the remainder of this post we will give an introductory survey of the basic principles of quantum mechanics and cover a few of its core ideas.
Preliminaries
In order to have a deep understanding and appreciation for the more nuanced ideas in quantum mechanics, one needs to have a substantial background in mathematics, physics, and at least a basic understanding of statistics. In this post, we will do our best to leap gracefully around some of these barriers at the risk of oversimplifying the underlying ideas. However, in order to even state some of the core ideas, we will assume that the reader is familiar with Calculus, some Linear Algebra, and at least has some idea of how complex numbers and probabilities work. If you are allergic to derivatives, or have a pathological fear of matrices, you may encounter some difficulty if you continue reading this post without reviewing some of these foundational ideas. Here are some online resources you may find helpful in refreshing your understanding:
Background Reading:
- Linear Algebra:
- MIT Open Courseware Linear Algebra (Dr. Gilbert Strang)
- Essence of Linear Algebra Video Series (3Blue1Brown)
- Linear Differential Equations:
- Linear Differential Equations Notes (Paul’s Online Notes)
- Differential Equations Video Series (3Blue1Brown)
- Statistics:
- Probability and Statistics (LibreTexts Physics)
The Schrodinger Equation
We will begin our introduction to quantum mechanics by examining one of its most fundamental equations: the Schrodinger equation. In order to derive this equation, we must first acquire a bit more intuition about simple wave-like systems. For example, consider the following wave function with frequency $\nu$ and wavelength $\lambda = h/p$:
\[\psi(x, t) = \exp\left(i2\pi\left[\frac{x}{\lambda} - \nu t\right]\right)\]Above, $i = \sqrt{-1}$ is the imaginary constant. This wave function $\psi(x,t)$ is the form of a general harmonic wave. It is complex-valued, and varies with both position $x$ and time $t$. If we plot the real and imaginary components of $\psi$ with respect to time, we find that these two components are both forward propagating harmonic waves (e.g. sine and cosine waves):
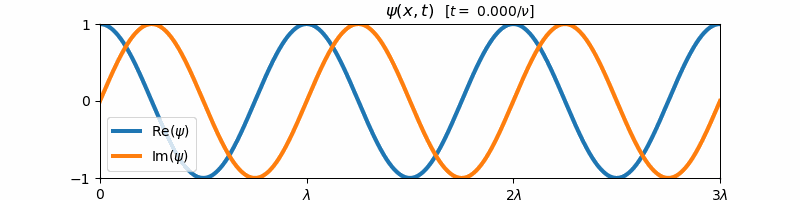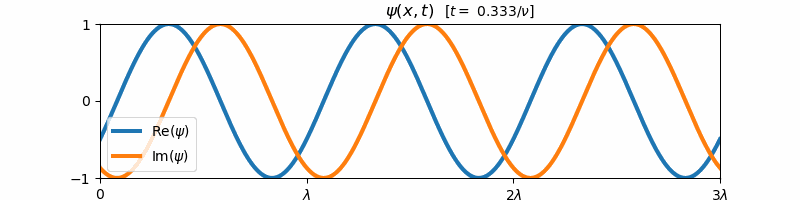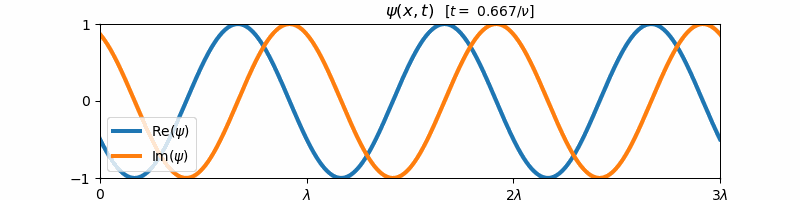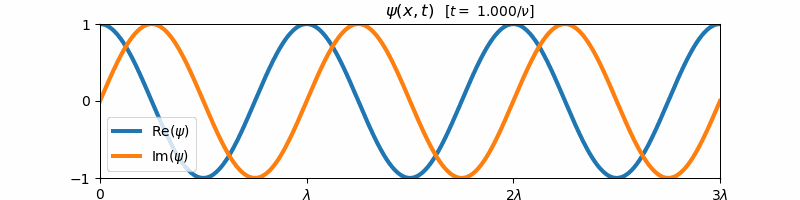
These sine and cosine waves arise as a result of Euler’s identity:
\[e^{i\theta} = \cos(\theta) + i\sin(\theta)\]For $\theta = 2\pi [x/\lambda - \nu t]$, we can re-write the form of $\psi(x,t)$ as a sum of its real and imaginary components:
\[\psi(x,t) = \cos\left(2\pi\left[\frac{x}{\lambda} - \nu t\right]\right) + i\sin\left(2\pi\left[\frac{x}{\lambda} - \nu t\right]\right)\]We say that a general harmonic wave is harmonic in both time and space, since the real and imaginary components of $\psi(x,t)$ vary sinusoidally with $x$ when $t$ is held constant and with $t$ when $x$ is held constant. Because of this, a general harmonic wave is characterized by two variables, the wave frequency $\nu$ and the wavelength $\lambda$. Note that the inverse wavelength $1/\lambda$ corresponds to the “spatial frequency” of the wave. We observe that $\nu$ and $1/\lambda$ are proportional to the partial derivative of $\psi$ with respect to time and space respectively:
\[\dfrac{\partial}{\partial t}\psi(x,t) = (-i2\pi \nu)\exp\left(i2\pi\left[ \frac{x}{\lambda} - \nu t \right]\right) = (-i2\pi \nu)\psi(x,t)\] \[\dfrac{\partial}{\partial x}\psi(x,t) = (i2\pi/\lambda)\exp\left(i2\pi\left[ \frac{x}{\lambda} - \nu t \right]\right) = (i2\pi/\lambda)\psi(x,t)\]The energy of this harmonic wave is given by Planck’s equation, $E = h\nu$. Substituting $E/h$ for $\nu$ in the expression for $\frac{\partial}{\partial t}\psi(x,t)$, we obtain:
\[\dfrac{\partial}{\partial t}\psi(x,t) = \frac{-i2\pi E}{h}\psi(x,t)\]To remove the factor of $2\pi$, we define the reduced Planck constant $\hbar = \frac{h}{2\pi}$. After some re-arranging, we obtain the form of the Schrodinger Equation:
\[\boxed{\dfrac{\partial}{\partial t}\psi(x,t) = \frac{-i}{\hbar}E\psi(x,t)}\]The Schrodinger equation is a linear partial differential equation that relates the measured energy $E$ of a wave function to its rate of change. Since there is an $i$ coefficient in the right hand side of the equation, solutions to the Schrodinger equation will oscillate in time with a frequency $\nu$ that satisfies Planck’s equation, $E = h\nu$. Specifically, for some initial wave function $\psi(x,0)$ measured to have energy $E$ at $t = 0$, the solution to the Schrodinger equation takes the form:
\[\psi(x,t) = \exp\left(\frac{-it}{\hbar}E\right)\psi(x,0)\]We observe that this solution to the Schrodinger equation is harmonic in time and oscillates with frequency $\nu = E/h$. However, an arbitrary wave function $\psi(x,t)$ that solves the Schrodinger equation is not always guaranteed to be harmonic with respect to space (as was the case with the general harmonic wave we have studied so far).
In the next section, we will investigate how we can determine the form of a particle’s initial wave function $\psi(x,0)$, based on its kinetic and potential energy.
The Hamiltonian Operator
We have derived the Schrodinger equation and shown that its solution corresponds to a time-harmonic wave function with respect to some initial spatial wave function $\psi(x,0)$. The next question we will consider is how we can determine the shape of $\psi(x,0)$. So far, we have examined the special case of the wave $\psi(x,t) = \exp(i2\pi[x/\lambda - \nu t])$. Specifically, we found that this function satisfied the spatial partial differential equation
\[\dfrac{\partial}{\partial x}\psi(x,t) = (i2\pi/\lambda)\psi(x,t)\]at all times $t$, including $t = 0$. Applying DeBroglie’s wave equation ($\lambda = h/p$), which we discussed earlier, we observe that the momentum $p$ of this wave is constant and inversely proportional to the wavelength $\lambda$:
\[\lambda = \frac{h}{p} = \frac{2\pi \hbar}{p}\]Substituting this into the spatial PDE, and re-arranging, we obtain an equation relating the wave function to its partial derivative with respect to $x$:
\[-i\hbar\dfrac{\partial}{\partial x}\psi(x,t) = p\psi(x,t)\]While the space-harmonic wave we are studying has constant momentum, this is not always the case. For arbitrary wave functions $\psi(x,t)$, the wave momentum can be expressed as a function of position and time. Specifically, this momentum function can obtained through applying the momentum operator $\hat{\mathbf{p}}$, defined by
\[\hat{\mathbf{p}} = -i\hbar\dfrac{\partial}{\partial x}.\]Applying $\hat{\mathbf{p}}$ to an arbitrary wave function $\psi(x,t)$, we obtain the momentum function $p(x,t)$, which must satisfy
\[p(x,t)\psi(x,t) = \hat{\mathbf{p}}\psi(x,t) = -i\hbar\dfrac{\partial}{\partial x}\psi(x,t).\]For wave functions corresponding to particles with mass $m$, we can also compute the particle’s kinetic energy $E_{KE}$. From classical physics, we recall the kinetic energy equation:
\[E_{KE} = \frac{1}{2}mv^2 = \frac{p^2}{2m}\]For arbitrary wave functions, the kinetic energy is also a function of position and time, and it must satisfy
\[E_{\text{KE}}(x,t)\psi(x,t) = \frac{\hat{\mathbf{p}}^2}{2m}\psi(x,t) = \frac{-\hbar^2}{2m}\dfrac{\partial^2}{\partial x^2}\psi(x,t).\]This describes a particle’s kinetic energy, but what about the potential energy? Typically, we assume that the potential energy is known function of position, denoted by $V(x)$. This potential energy function accounts for potential energy due to effects such as interactions with charged particles.
Since total energy in any physical system is conserved, it must be the case that the sum of the kinetic and potential energies must equal the total energy of a wave function. To compute the total energy of an arbitrary wave function, we introduce the Hamiltonian operator $\hat{\mathbf{H}}$ as follows:
\[\hat{\mathbf{H}} \equiv (\text{kinetic energy}) + (\text{potential energy}) \equiv \frac{\hat{\mathbf{p}}^2}{2m} + V(x,t)\]The Hamiltonian operator is named after William Rowan Hamilton, a physicist who developed a formulation of classical mechanics by introducing operators that use the sum of the kinetic and potential components of a system’s total energy to describe its dynamics. Despite its origin as an operator in classical physics, the Hamiltonian operator formalism is quite useful in describing the time evolution of quantum systems as well.
The Hamiltonian operator is quite useful in determining the initial shape of a wavefunction $\psi(x,t)$. If a wavefunction is measured to have energy $E$ at time $t = 0$, the law of conservation of energy requires that the kinetic and potential components of the wave function’s energy sums to $E$ at every point $x$ in space. This means that
\[\boxed{E\psi(x,0) = \hat{\mathbf{H}}\psi(x,0) = \frac{-\hbar^2}{2m} \dfrac{\partial^2}{\partial x^2}\psi(x,0) + V(x)\psi(x,0)}\]must hold for every point $x$ in space. Solving for the initial wave function $\psi(x,0)$ that satisfies this linear partial differential equation is not an easy task. Closed-form solutions to this equation can be found for simple potentials $V(x)$, but with more complex potentials the equation must be solved numerically. Also, for some potential functions $V(x)$, there are only discrete values of $E$ that can satisfy this equation. This discretization of “allowed” energy levels is an important concept we will return to later.
To the attentive reader, the fact that the total energy $E$ must be constant for all values of $x$ may seem a bit confusing, especially considering that we previously claimed the wave function’s kinetic energy $E_{KE}(x,t)$ was a function of position and time. The reason that $E$ is independent of $x$ at $t = 0$ is because we have measured the energy of the system at time $t = 0$. The concept of measurement is an important part of the theory of quantum mechanics, and we will discuss it in greater detail in a future post. For now, we will assume that when a a particle’s energy is measured, the particle’s wave function “collapses” to one where $E$ is a constant value that is essentially independent of space.
We know from earlier that if a wave function is measured to have energy $E$ at time $t = 0$, it will evolve in time according to the solution to the the Schrodinger equation, $\psi(x,t) = e^{-itE/\hbar}\psi(x,0)$. Since the Hamiltonian operator $\hat{\mathbf{H}}$ is a linear operator, it commutes with multiplication by scalars such as $E$ and $e^{-itE/\hbar}$. Thus, it follows that:
\[\begin{aligned} \hat{\mathbf{H}}\psi(x,t) &= \hat{\mathbf{H}}e^{-itE/\hbar}\psi(x,0) \\ &= e^{-itE/\hbar}\hat{\mathbf{H}}\psi(x,0) \\ &= e^{-itE/\hbar}E\psi(x,0) \\ &= Ee^{-itE/\hbar}\psi(x,0) \\ &= E\psi(x,t)\end{aligned}\]This means that if $\hat{\mathbf{H}}\psi(x,0) = E\psi(x,0)$ at $t = 0$, then $\hat{\mathbf{H}}\psi(x,t) = E\psi(x,t)$ for all times $t > 0$. This reflects the idea that the total energy of the wave function is conserved in time. We can also use this equivalence to write down the more general form of the Schrodinger equation that is independent of the energy $E$ measured at $t = 0$:
\[\boxed{\dfrac{\partial}{\partial t}\psi(x,t) =\frac{-i}{\hbar}\hat{\mathbf{H}}\psi(x,t)}\]Remarkably, it can be shown that this equation always holds, even if the system’s energy is not measured to be some constant value $E$ at $t = 0$. However, we will discuss some of these more nuanced insights in a future post.
Conclusion
In this post, we gave a basic introduction to the Schrodinger equation. We derived it by exploring the physics of waves that are harmonic in time and space. Although it can be derived by studying these harmonic waves, the Schrodinger equation is remarkably flexible and can describe the dynamics of most quantum-mechanical systems. To find the shapes of these wave functions in space, we introduced the Hamiltonian operator $\hat{\mathbf{H}}$, and observed that waves $\psi(x,t)$ with a measured energy $E$ must satisfy the equation $E\psi(x,t) = \hat{\mathbf{H}}\psi(x,t)$. Finally, we used the Hamiltonian operator to derive the more general form of the Schrodinger equation, which is independent of a wave’s measured energy $E$.
In the next post, we will discuss wave functions in greater detail. We will also discuss the important concept of linearity in quantum mechanics and develop some additional intuition regarding linear operators.
